题目中有些元素或者位置有特殊的要求,可以优先去考虑有特殊要求的元素或者位置。
【例1】张老师要将3本不同的外文书、1本科技书和2本不同的计算机书摆成一排在书架上,若科技书必须放在两端,则有多少种不同的摆放顺序?
A.480
B.240
C.120
D.60
答案:B
【解析】本题考查排列组合问题,用优限法解决。首先考虑3种书中有特殊排位要求的科技书,只能放在两端,有2种方法;另外5本书排列没有任何要求,我们将其全排,有A(5,5)种;那么此题我们分步考虑,最终有2(A(5,5))=240种,选B。
二、捆绑法
题目中有元素要求相邻,将要求相邻的元素捆绑成一个整体参与计算,必要时考虑捆绑在一起的元素内部的顺序。
【例2】由数字1、2、3、4、5组成无重复数字的五位数,所有奇数必须相邻的五位数有( )个。
A.36
B.48
C.60
D.72
答案:A
【解析】该题目要求所有奇数相邻,也就是1,3,5必须在一起,可以使用捆绑法进行分析。我们将1,3,5看成一个整体,也就是可以把1,3,5看成“一个数字”,再将这“一个数字”和剩下的2个数字进行排列,这样就相当于三个数字对应三个不同的位置,同时我们也要注意1,3,5这三个相邻的数字它们内部之间也有顺序要求,先考虑整体,再考虑捆绑内部,是一个分步过程,所求为6×6=36。选择A。
三、插空法
题目中有些元素要求不相邻,可先排列无位置要求的元素,再把要求相邻的元素插入上述元素的空位中。
【例3】一次小型文艺演出活动上有2个舞蹈节目,2个小品,2个唱歌节目。在制定节目顺序时,要求2个唱歌节目不能相邻演出,则共有多少种不同的演出顺序?
A.120
B.240
C.480
D.720
答案:C


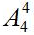 种排法;最后将2个唱歌节目插在其余4个节目所形成的5个空隙中,有
种排法;最后将2个唱歌节目插在其余4个节目所形成的5个空隙中,有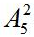 种方法;故共有
种方法;故共有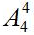 ×
×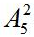 =24×20=480种不同的演出顺序。故选C。
=24×20=480种不同的演出顺序。故选C。 申论太难没学会?扫码回复“咨询老师”
申论太难没学会?扫码回复“咨询老师”
